2023年成考专升本每日一练《高等数学二》11月7日专为备考2023年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、广义积分 ()
()
- A:
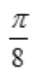
- B:
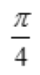
- C:
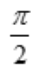
- D:π
答 案:B
解 析: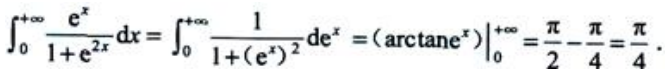
2、函数f(x)在[0,2]上连续,且在(0,2)内f'(x)>0,则下列不等式成立的是().
- A:f(0)>f(1)>f(2)
- B:f(0)<f(1)<f(2)
- C:f(0)<f(2)<f(1)
- D:f(0)>f(2)>f(1)
答 案:B
解 析:由题意知函数f(x)在(0,2)内单调递增,故f(0)<f(1)<f(2).
主观题
1、计算
答 案:解:
2、若f(x)的一个原函数为xsinx,求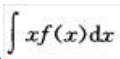 .
.
答 案:解:因为f(x)的一个原函数为xsinx,所以 因此
因此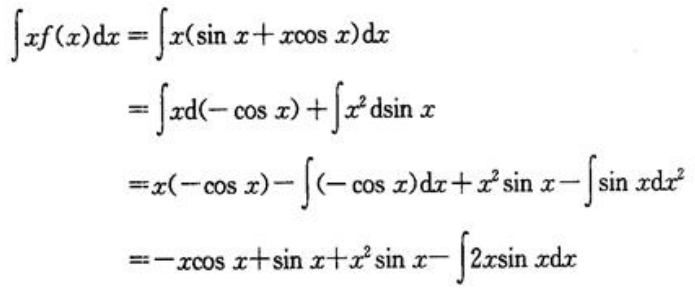
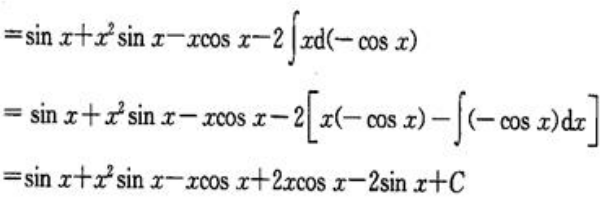
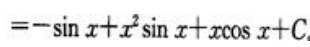 .
.
填空题
1、两封信随机投入标号为1,2,3,4的四个邮筒,则1,2号邮筒各有一封信得概率为().
答 案: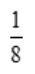
解 析:每封信有4种投法,共有42种投法,1,2号邮筒各一封信的情况有2种,故其概率为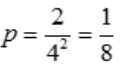 .
.
2、二元函数z=xy在x+y=1下的极值为()
答 案: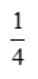
解 析:化为无条件极值,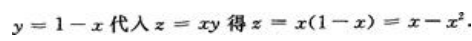 又因
又因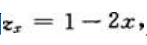 则令
则令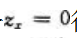 得驻点
得驻点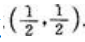 当
当 时,zx>0;当时zx<0,故该点
时,zx>0;当时zx<0,故该点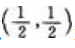 是极大值点且极大值
是极大值点且极大值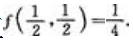
简答题
1、设函数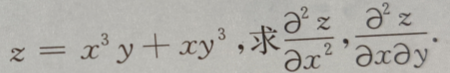
答 案: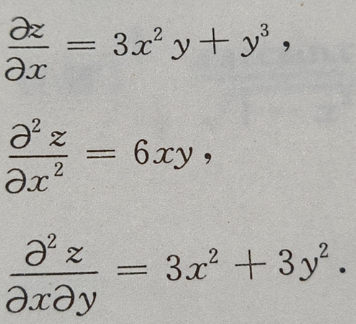
2、证明: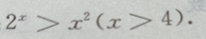
答 案:令 则
则 由于此式不便判定符号,故再求出
由于此式不便判定符号,故再求出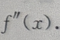 又因
又因
 所以f'(x)单调增加,故f'(x)>f'(4)=
所以f'(x)单调增加,故f'(x)>f'(4)= -8=8(2ln2-1)=8(ln4-1)>0, 得到f(x)单调增加,故f(x)>f(4),即
-8=8(2ln2-1)=8(ln4-1)>0, 得到f(x)单调增加,故f(x)>f(4),即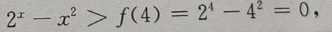 因此
因此
精彩评论