2025年成考高起点每日一练《数学(文史)》4月3日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知f(x)=ax²+b的图像经过点（1,2）且其反函数f^-1（x）图像经过点（3,0），则函数f（x）的解析式是（）。

• A：
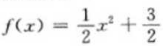
• B：f(x)=-x²+3
• C：f(x)=3x²+2
• D：f(x)=x²+3

答 案：B

解 析：∵f(x)的反函数f^-1（x）过点（3,0），所以f(x)又过点（3,0），所以有f（1）=2，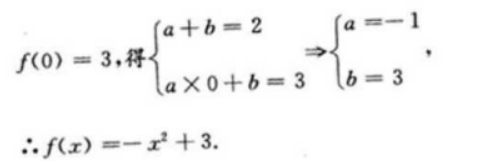

2、下列函数中，既是偶函数，又在区间（0，3）为减函数的是（）。

• A：y=cosx
• B：y=log2^x 
• C：
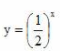
• D：y=x²-4

答 案：A

3、设集合M={a，b，c，d}，N=（a，b，c），则集合M∪N=（）。  

• A：{a，b，c}
• B：{d}
• C：{a，b，C，d}
• D：空集

答 案：C

4、函数y=-x²+2x的值域是（）。  

• A：[0,+∞)
• B：[1,+∞)
• C：(-∞,1]
• D：(-∞,0)

答 案：C

解 析：本题主要考查的知识点为函数的值域. y=-x²+2x=1-(x-1)²≤1，故原函数的值域为(-∞,1]

主观题

1、已知x+x^-1=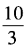，求x²+x^-2的值。  

答 案：由已知，得

2、设3^a=5^b=15，求a^-1+b^-1的值。  

答 案：由3^a=15，得a=log₃15；又由5^b=15，得b=log₅15。 因此a^-1+b^-1=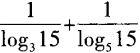 =log₁₅3+log₁₅5=1。

解 析：过程中应用了换底公式的推论，即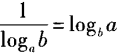

3、已知函数f（x）=2x³-3x²，求
（1）函数的单调区间；

（2）函数f（x）在区间[-3，2]的最大值与最小值。

答 案：

4、等差数列{an}的通项公式为an=3n-1，在{an}中，每相邻的两项之间插人三项，构成新的等差数列{bn}． (Ⅰ)求{bn}的通项公式； (Ⅱ)求{bn}前10项的和．

答 案： 考点本题主要考查等差数列的通项公式和前n项和公式的运用，是成人高考常见题型．

填空题

1、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。  

答 案：45

2、函数y=2cosx-cos2x（x∈R）的最大值为______。  

答 案：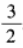

解 析：