2025年成考高起点每日一练《数学(理)》4月6日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、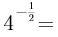 ( )
( )
- A:-2
- B:
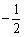
- C:
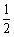
- D:2
答 案:C
2、中心在坐标原点,一个焦点的坐标是(-3,0),一条渐近线方程式 的双曲线方程是()。
的双曲线方程是()。
- A:
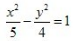
- B:
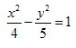
- C:
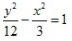
- D:
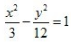
答 案:B
3、函数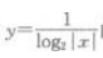 定义域为()。
定义域为()。
- A:{z|x≠0,x∈R}
- B:{x|x≠±1,x∈R}
- C:{x|x≠0,x≠±1,x∈R}
- D:{x|x∈R}
答 案:C
解 析:|x|>0,且|x|=1,得x≠0,且x≠±1。答案为C。
4、设f(x)=x3+ax2+x为奇函数,则a=()。
- A:1
- B:0
- C:
- D:-2 D.C.-1
答 案:B
解 析:本题主要考查的知识点为函数的奇偶性. 因为f(x)为奇函数,故f(-x)=-f(x)。即-x3+ax2-x=-x3-ax2-x,a=0。
主观题
1、设函数f(x)= (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案:(Ⅰ)函数的定义域为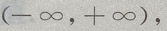
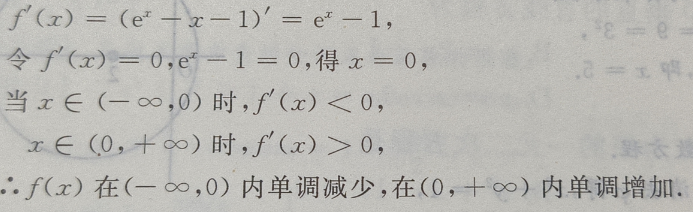 (Ⅱ)
(Ⅱ)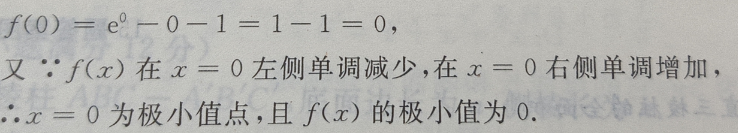
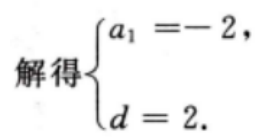
2、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
答 案:因为{an}为等差数列,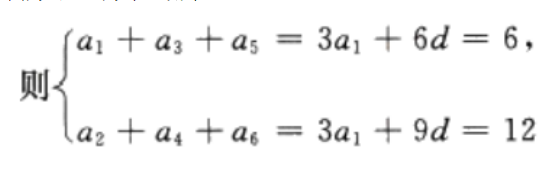
3、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得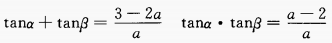

4、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
填空题
1、一个问题在1小时内,甲能独立解决的概率是0.5,乙能独立解决的概率是0.4,两人在1小时内解决问题的概率是______。
答 案:0.7
解 析:设事件A为两人在1小时内解决问题,即1小时内至少有一人能解决问题,事件B为甲在1小时内解决问题,事件C为乙在1小时内解决问题,事件B、C是相互独立事件,事件A的对立事件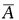 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(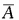 )=1-P(
)=1-P(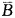 ·
·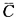 )=1-P(
)=1-P(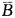 )·P(
)·P(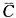 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
2、在△ABC中,a=2,b=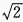 ,∠B=
,∠B=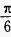 ,则∠A=______。
,则∠A=______。
答 案:
解 析: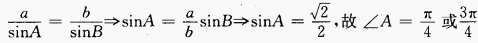
精彩评论