2025年成考专升本每日一练《高等数学二》4月9日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、已知y=2x+x2+e2,则y’等于()。
- A:
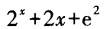
- B:
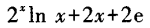
- C:
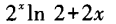
- D:
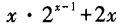
答 案:C
解 析:用基本初等函数的导数公式。
2、若事件A与B满足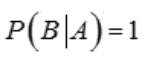 ,则有().
,则有().
- A:A是必然事件
- B:
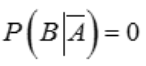
- C:
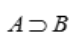
- D:

答 案:D
解 析:由题意 ,当
,当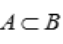 时
时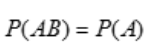 满足条件.
满足条件.
主观题
1、每次抛掷一枚骰子(6个面上分别标有数字1、2、3、4、5、6),连续抛掷2次,设A={向上的数字之和为6},求P(A).
答 案:解:基本事件数为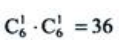 抛掷两次,向上的数字之和为6的事件共有5种,即(1,5),(2,4),(3,3),(4,2),(5,1).注意事件(1,5)与(5,1)是两个不同的事件:第一次出现1或5而第二次出现5或1是两个不同的结果,所以P(A)=
抛掷两次,向上的数字之和为6的事件共有5种,即(1,5),(2,4),(3,3),(4,2),(5,1).注意事件(1,5)与(5,1)是两个不同的事件:第一次出现1或5而第二次出现5或1是两个不同的结果,所以P(A)= .
.
2、证明:当x>0时,
答 案:证:令 ,
,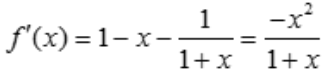 ,令
,令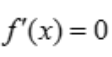 ,得x=0,f(0)=0,当x>0时,f'(x)<0,故函数单调递减,
,得x=0,f(0)=0,当x>0时,f'(x)<0,故函数单调递减,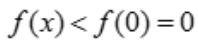 ,则
,则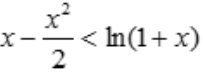 .令
.令 ,
,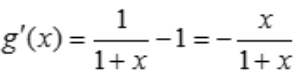 ,令
,令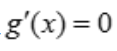 ,得x=0,g(0)=0,当x>0时,f'(x)<0,故函数单调递减,f(x)<f(0)=0,则
,得x=0,g(0)=0,当x>0时,f'(x)<0,故函数单调递减,f(x)<f(0)=0,则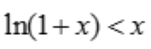 .综上得,当x>0时,
.综上得,当x>0时,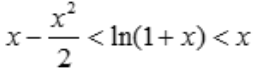 .
.
填空题
1、若点(1,3)是曲线y=ax3+bx3拐点,则a,b分别为().
答 案: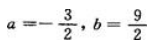
解 析:因点(1,3)在曲线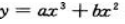 上,所以a+b=3.又因
上,所以a+b=3.又因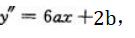 所以6a+2b=0.解方程组
所以6a+2b=0.解方程组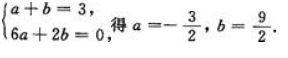
2、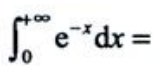 ().
().
答 案:1
解 析: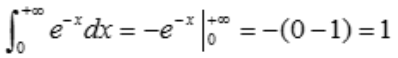 .
.
简答题
1、盒中有5个球,其中3个白球,2个黑球,从中随机一次抽取3个球,用X表示抽取到的白球的个数。 (1)求随机变量X的概率分布;
(2)求X的数学期望E(X).
答 案:
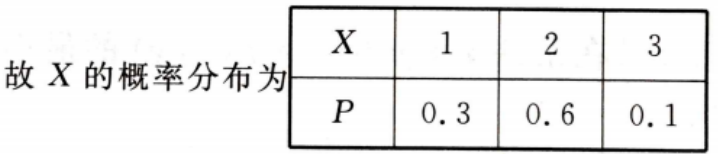 (2)E(X)=1x0.3+2x0.6+3x0.1=1.8.
(2)E(X)=1x0.3+2x0.6+3x0.1=1.8.
2、已知曲线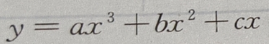 在点(1,2)处有水平切线,且原点为该曲线的拐点,求a,b,c的值,并写出此曲线的方程。
在点(1,2)处有水平切线,且原点为该曲线的拐点,求a,b,c的值,并写出此曲线的方程。
答 案:
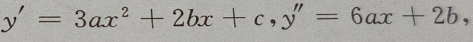 由已知条件得:
由已知条件得:
 故b=0,a=-1,c=3,次曲线的方程为
故b=0,a=-1,c=3,次曲线的方程为
精彩评论