2025年成考高起点每日一练《数学(理)》4月17日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、与1775°的终边相同的绝对值最小的角是（）。

• A：335°
• B：-25°
• C：25°
• D：155°

答 案：B

解 析：1775°=5×360°+（-25°），故所求角为-25°。  

2、函数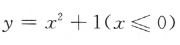的反函数是（）

• A：
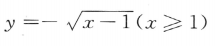
• B：
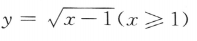
• C：
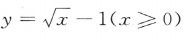
• D：

答 案：A

解 析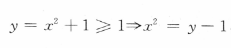：，由于x≤0，故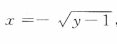把x与y互换，得所求反函数为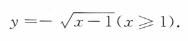

3、若f(x＋1)＝x²－2x＋3，则f(x)＝（）。

• A：x²＋2x＋6
• B：x²＋4x＋6
• C：x²－2x＋6
• D：x²－4x＋6

答 案：D

解 析：f(x＋1)＝x²－2x＋3＝(x＋1)²－4(x＋1)＋6，∴f(x)＝x2－4x＋6。(答案为D)

4、直线2x+y+m=0和直线x+2y+n=0的位置关系是（）。

• A：平行
• B：垂直
• C：相交但不垂直
• D：不确定

答 案：C

解 析：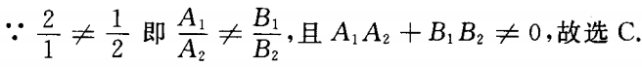

主观题

1、函数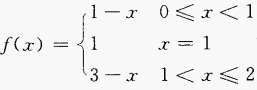在其定义域上是否连续？作出f（x）的图形。

答 案：f（x）的定义域为[0，2] 当0≤x<1时f（x）=1-x是连续的 当1 f(x)除了在x=1处不连续,在其定义域内处处连续,如图7-7.

2、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得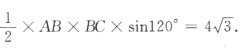所以AB =4.因此所以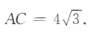

3、求将抛物线y=x²-2x-3平移到顶点与坐标原点重合时的函数解析式。  

答 案：

4、化简： （1）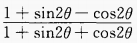
（2）

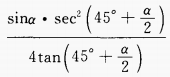
答 案：（1） （2）

填空题

1、若tanα-cotα=1，则=______。

答 案：4

解 析：由立方差公式得,tan³α-cot³α=(tana-cotα)(tan²α+tanαcota+cot²α)(tana-cotα)[(tanα-cotα)²+3tanαcotα]=4  

2、已知≤0＜2π，且实数x满足log₃x=2-cos²θ+sin²θ，则x的最小值是______。  

答 案：3

解 析：因为log₃x=2-（cos²θ-sin²θ）=2-cos2θ。 又log₃x中的底数3＞1，因此要使x最小，应使2-cos2θ的值最小，而其最小值为1，故x=3。