2025年成考高起点每日一练《数学(文史)》4月20日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、函数f(x)=x3-6x2+9x-3的单调区间为()。
- A:(-∞,-3),(-3,1),(1,+∞)
- B:(-∞,-1),(-1,3),(3,+∞)
- C:(-∞,-3),(-3,-1),(-1,+∞)
- D:(-∞,1),(1,3),(3,+∞)
答 案:D
解 析:∵x∈R
f’(x)=3x2-12x+9
=3(x2-4x+3)
=3(x-3)(x-1)
∴x>3或x<1,f’(x)>0,
1 2、一枚硬币连抛3次,至少有两次正面向上的概率是()。 答 案:A 解 析:此题一枚硬币连抛3次等价于3枚硬币抛一次,这种试验的等可能结果总数n=8,其至少两次正面向上的结果总数m=4,故所求概率为 3、点P(2,5)到直线x+y-9=0的距离是() 答 案:C 解 析:根据点到直线的距离公式得,P(2,5)到直线x+y-9=0的距离为 4、设集合A={x|x2-2x-32},则A∩B=( ) 答 案:A 主观题 1、已知三角形的三边边长组成公差为1的等差数列,且最大角是最小角的二倍,求三边之长。
答 案:三角形的三边边长分别为4,5,6。 2、如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)
答 案:如图 3、已知等差数列 答 案:(Ⅰ)当n=1时,由 4、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 填空题 1、函数y= 答 案:[1,+∞) 解 析:要是函数y= 2、函数f(x)= 答 案:4 解 析:这题考的是高次函数的最值问题,可用导数来求函数在区间[-3,3]上的最值。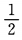
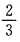
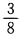
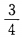
 ,故应选A。
,故应选A。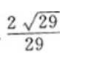
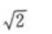
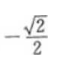
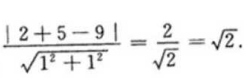

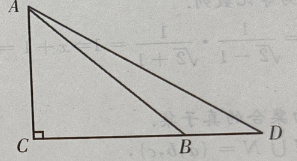
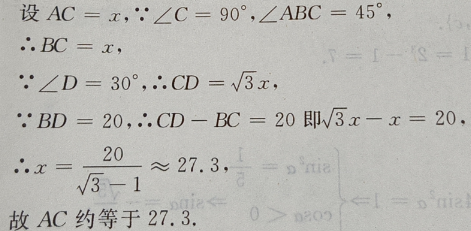
 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项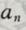 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求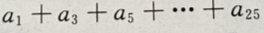 的值
的值
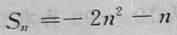 得
得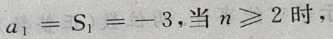
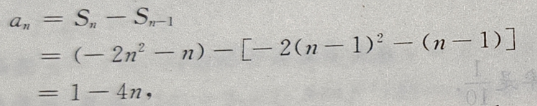
 也满足上式,故
也满足上式,故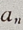 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列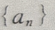 是首项为
是首项为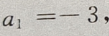 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以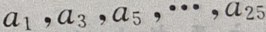 是首项为
是首项为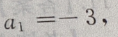 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

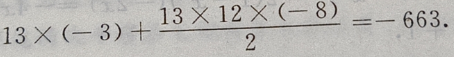

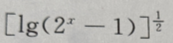 的定义域是()
的定义域是() 有意义,需使
有意义,需使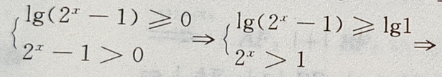
 所以函数的定义域为{x|x≥1}=[1,+∞)
所以函数的定义域为{x|x≥1}=[1,+∞)
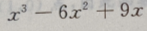 在区间[-3,3]上的最大值为()
在区间[-3,3]上的最大值为()
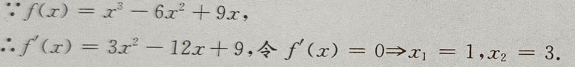 列出表格
列出表格 由上表可知函数在[-3,3]上,在x=1点处有最大值为4.
由上表可知函数在[-3,3]上,在x=1点处有最大值为4.
精彩评论