2025年成考高起点每日一练《数学(文史)》4月21日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、cos12°cos98°-sin12°sin98°=（）。

• A：cos20°
• B：sin20°
• C：-cos20°
• D：-sin20°

答 案：D

解 析：原式=cos110°=cos（180°-70°）=-cos70°=-cos（90°-20°）=-sin20°。  

2、y=(2x²+3)(3x-2)的导数是（　）

• A：18x²-8x+9
• B：6x²+9
• C：12x²-8x
• D：12x

答 案：A

解 析：y=(2x²+3)(3x-2)=6x³-4x2+9x-6，y´=18x²-8x+9．【考点指要】会用两个函数和、差的求导法则求多项式函数的导数，是近几年成人高考的常见题．

3、下列函数中，为减函数的是（）

• A：y=cosx
• B：
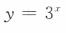
• C：
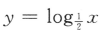
• D：

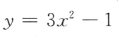
答 案：C

解 析：由对数函数的性质可知，当底数大于0小于1时，在定义域内，对数函数为减函数，故选C选项．

4、已知向量i,j为互相垂直的单位向量，向量a=2i+mj，若|a|=2，则m=（）

• A：-2
• B：-1
• C：0
• D：1

答 案：C

解 析：由题可知a=(2,m),因此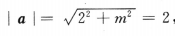，故m=0.

主观题

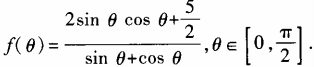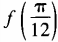1、设函数 （1）求；（2）求函数f（θ）最小值。

答 案：

2、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．

答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积

3、在△ABC中，已知AB=2,BC=1,CA=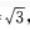 点D,E,F分别在AB,BC,CA边上，△DEF为正三角形，记∠FEC为α，如果sinα= 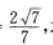求△DEF的边长。

答 案：解析:由AB=2，BC=1,CA=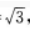 得BC²=CA²=AB²,因此∠C=90°，如图所示。 因为sinA= 所以∠A=30°，于是∠b=60°。 设正△DEF边长为l，已知AB=2,sinα=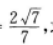 由此EC=lcosα 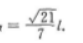有图知，∠1+∠2+∠3=180°（三角形内角和）； ∠3+∠4+α=180°，因为∠2-∠4=60°，所以∠1=α。 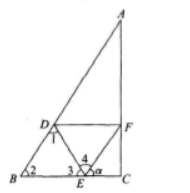【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理，这些均是考试大纲要求掌握的重要概念，并要求能达到灵活应用的程度，此类题是在成人高考中出现频率较高的题型，

4、已知F是椭圆的右焦点，点M在抛物线y2=2px（p＞0）上O为坐标原点，且△MOF为正三角形．  (Ⅰ)求P的值； (Ⅱ)求抛物线的焦点坐标和准线方程．

答 案：(Ⅰ)由椭圆方程可知，椭圆的长半轴a=5，短半轴，则椭圆的半焦距 即椭圆的右焦点F的坐标为 (4.0). 如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点， 【考点指要】本题主要考查椭圆、抛物线的概念，要求考生掌握它们的标准方程和性质，会用它们解决有关的问题．  

填空题

1、已知α+β=π/4，则（1+tanα）（1+tanβ）=______。  

答 案：2

2、为了考察某种小麦的长势，从中抽取10株苗，测得苗高如下(单位：cm)：12,13，14，15，10，16，13，11，15，11． 则该品种的小麦苗高的样本方差为__________cm2．

答 案：3.6

解 析：由题中条件可得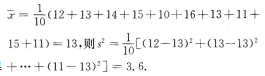 【考点指要】本题主要考查样本的平均值和方差的计算，考生只需熟记样本平均数和方差的公式即可．