2025年成考高起点每日一练《数学(文史)》4月22日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、用列举法表示集合{（x，y）|x+2y=7且x，y为正整数}，结果是（）。  

• A：{x=5，3，1，y=1，2，3}
• B：{（5，1），（3，2）（1，3）}
• C：{（1，5），（2，3），（3，1）}
• D：{（7，0）（5，1）（3，2）（1，3）}

答 案：B

2、与圆x2+y2=4关于点M（3,2）成中心对称的曲线方程是（）

• A：（x-3）2+（y-2）2=0
• B：（x+3）2+（y+2）2=0
• C：（x-6）2+（y-4）2=0
• D：（x+6）2+（y+4）2=0

答 案：C

解 析：与圆关于点M成中心对称的曲线还是圆.只要求出圆心和半径，即可求出圆的方程.圆X2+y2=4的圆心(0，0)关于点M(3,2)成中心对称的点为(6,4),所以所求圆的圆心为(6,4),半径与对称圆的半径相等，所以所求圆的方程为(x-6)2+(y-4)2=4。  

3、已知△ABC中，已知AB=2，AC=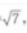BC=3，则∠B等于（）。

• A：
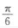
• B：
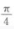
• C：
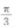
• D：

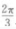
答 案：C

4、数列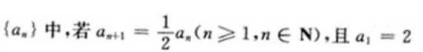则前5项的和是（）。

• A：-31/8
• B：31/32
• C：-31/32
• D：31/8

答 案：D

解 析：

主观题

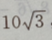1、已知三角形的一个内角是，面积是周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，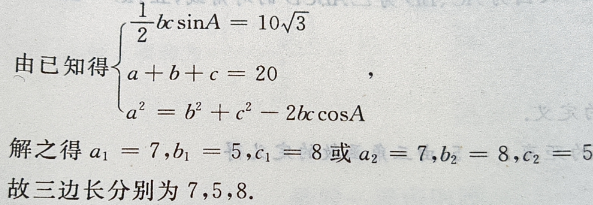  

2、求函数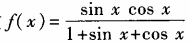（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

3、求下列函数的最大值、最小值和最小正周期： （1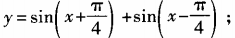） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

4、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图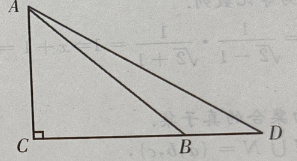  

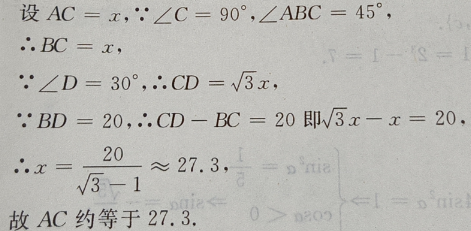
填空题

1、化简sin（x+y）-2cosxsiny=______。  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）  

2、某人投篮每次命中率为0.8，现独立投篮4次，恰好命中3次的概率是______。  

答 案：0.4096

解 析：本题试验属于独立重复试验，其概率为