2025年成考高起点每日一练《数学(理)》4月23日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、过点P(2,3)且在两轴上截距相等的直线方程为()
- A:
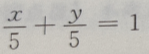
- B:
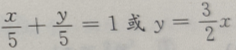
- C:x+y=5
- D:
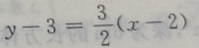
答 案:B
解 析:选项A中,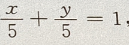 在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,
在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,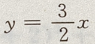 在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为:
在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为: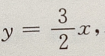 答案不完整
答案不完整
2、设F1和F2为双曲线的两焦点,点P在双曲线上,则||PF2|-|PF2||=()。
- A:4
- B:2
- C:1
- D:
答 案:A
解 析:由题意有a2=4.a=2,由双曲线的定义,可知||PF2|-|PF2||=2a=4.(答案为A)
3、在△ABC中,若lgsinA-lgsinB-lgcos=lg2,则△ABC是()
- A:以A为直角的三角形
- B:b=c的等腰三角形
- C:等边三角形
- D:钝角三角形
答 案:B
解 析:判断三角形的形状,条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2,由对数运算法则可得,左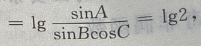 两个对数底数相等则真数相等:
两个对数底数相等则真数相等: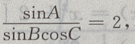 即2sinBcosC=sinA
在△ABC中,∵A+B+C=180°,∴A=180°-(B+C),
即2sinBcosC=sinA
在△ABC中,∵A+B+C=180°,∴A=180°-(B+C),
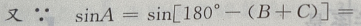
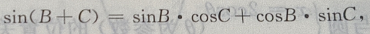
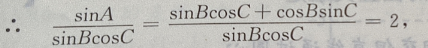
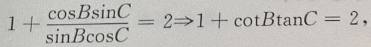
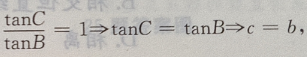 故为等腰三角形
故为等腰三角形
4、命题甲:实数a,b,c成等比数列;命题乙:b2=ac,则甲是乙()。
- A:充分条件但不是必要条件
- B:必要条件但不是充分条件
- C:充分必要条件
- D:不是充分条件也不是必要条件
答 案:A
主观题
1、计算。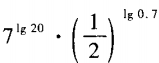
答 案: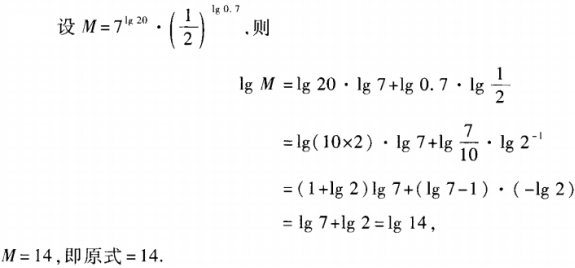
2、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 关于基底{a,b,c}的分解式
(Ⅱ)求证:
关于基底{a,b,c}的分解式
(Ⅱ)求证: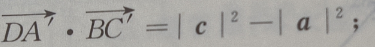 (Ⅲ)求证:
(Ⅲ)求证: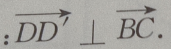
答 案:(Ⅰ)由题意知(如图所示) 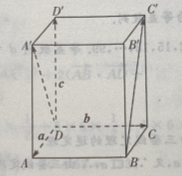
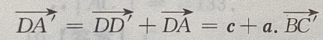
 (Ⅱ)
(Ⅱ)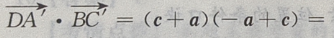
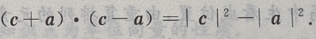 (Ⅲ)
(Ⅲ)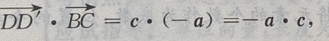 由已知,a,c是正四棱柱的棱,a,b,c两两垂直
由已知,a,c是正四棱柱的棱,a,b,c两两垂直

3、已知数列{an}中,a1=2,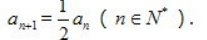 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
答 案:解:
4、已知空间四边形OABC,OB=OC且∠AOB=∠AOC=θ(如图)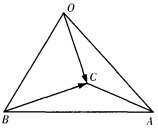 。求证:OA⊥BC。
。求证:OA⊥BC。
答 案:
填空题
1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。
答 案:85
解 析:本题主要考查的知识点为中位数. 将成绩按由小到大排列:63,77,79,81,85,88,89,94,99.因此中位数为85。
2、已知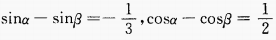 ,则
,则 =______。
=______。
答 案: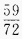
解 析: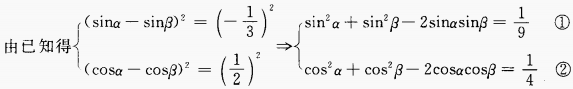
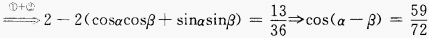
精彩评论