2025年成考高起点每日一练《数学(文史)》4月26日专为备考2025年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、直线绕原点按逆时针方向旋转30°后所得直线与圆（x-2）²+y²=3的位置关系是（）。

• A：直线过圆心
• B：直线与圆相交，但不过圆心
• C：直线与圆相切
• D：直线与圆相离

答 案：C

2、函数y=cos2x的最小正周期是（）。  

• A：6π
• B：4π
• C：2π
• D：π

答 案：D

3、（）。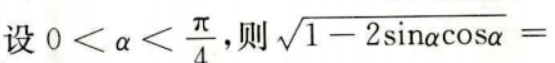

• A：sinα+cosα
• B：-sinα—cosα
• C：sinα—cosα
• D：cosα—sinα

答 案：D

解 析：本题主要考查的知识点为三角函数的运算。 当时，cosα>sinα>0，所以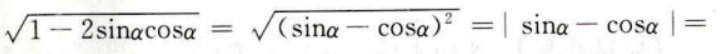

4、函数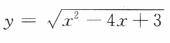的定义域是（）

• A：{x|-3≤x≤-1}
• B：{x|x≤-3或x≥-1}
• C：{x|1≤x≤3}
• D：{x|x≤1或x≥3}

答 案：D

解 析：由题可知x²-4x+3≥0，解得x≥3或x≤1，故函数的定义域为{x|x≤1或x≥3}.

主观题

1、已知a^m=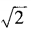，aⁿ=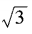，求a^3n-4m的值。  

答 案：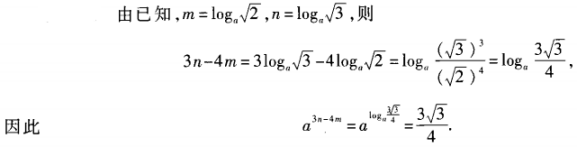

2、已知函数f（x）=2x³-3x²，求
（1）函数的单调区间；

（2）函数f（x）在区间[-3，2]的最大值与最小值。

答 案：

3、等差数列{an}的通项公式为an=3n-1，在{an}中，每相邻的两项之间插人三项，构成新的等差数列{bn}． (Ⅰ)求{bn}的通项公式； (Ⅱ)求{bn}前10项的和．

答 案： 考点本题主要考查等差数列的通项公式和前n项和公式的运用，是成人高考常见题型．

4、已知等差数列前n项和 （Ⅰ）求通项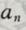的表达式 （Ⅱ）求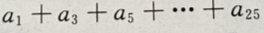的值  

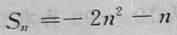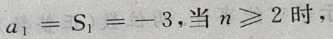
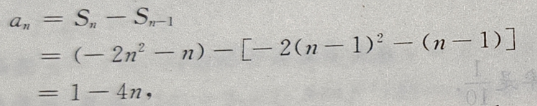
答 案：（Ⅰ）当n=1时，由得 也满足上式，故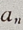=1-4n（n≥1） （Ⅱ）由于数列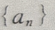是首项为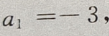公差为d=-4的等差数列，所以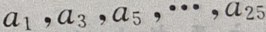是首项为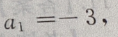公差为d=-8，项数为13的等差数列，于是由等差数列前n项和公式得：  

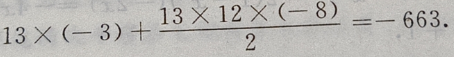
填空题

1、函数y=-x²+ax图像的对称轴为x=2，则a=______。

答 案：4  

解 析：本题主要考查的知识点为二次函数的性质。 由题意，该函数图像的对称轴为得a=4。

2、已知关于t的二次方程t²-6tsinθ+tanθ=0（0＜θ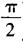＜）的两根相等，则sinθ+cosθ的值等于______。  

答 案：

解 析：