2025年成考高起点每日一练《数学(理)》5月5日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、在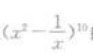 的展开式中,含x5项的系数是()。
的展开式中,含x5项的系数是()。
- A:1
- B:-1
- C:252
- D:-252
答 案:D
解 析: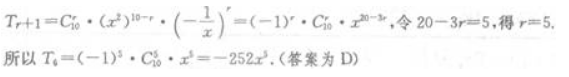
2、三个数0,30.7,log30.7的大小关系是()。
- A:0<30.7<log30.7
- B:log30.7<0<30.7
- C:log30.7<30.7<0
- D:0<log30.7<30.7
答 案:B
3、某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为()
- A:0.008
- B:0.104
- C:0.096
- D:1
答 案:B
解 析:已知灯泡使用1000小时后好的概率为0.2,坏的概率为1-0.2=0.8,则三个灯泡使用1000小时以后,可分别求得: P(没有坏的)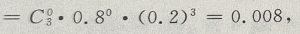 P(一个坏的)
P(一个坏的)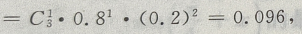 故最多只有一个坏的概率为:0.008+0.096=0.104.
故最多只有一个坏的概率为:0.008+0.096=0.104.
4、函数y=log3(x+1)的反函数为()。
- A:y=3x-1
- B:y=3x+1
- C:y=3x-1
- D:y=3x+1
答 案:C
解 析:由 y=log3(x+1),得x+1=3y,即 x=3y-1,函数 y=log3(x+1)的反函数为 y=3x-1(答案为C)
主观题
1、已知空间四边形OABC,OB=OC且∠AOB=∠AOC=θ(如图)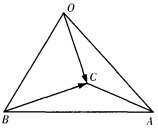 。求证:OA⊥BC。
。求证:OA⊥BC。
答 案:
2、已知am=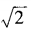 ,an=
,an=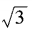 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: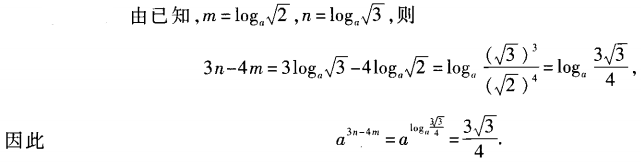
3、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程;
(II)求f(x)的极值.
答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
4、cos20°cos40°cos80°的值。
答 案:
填空题
1、已知A(0,1),B(1,2),存在一点P是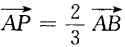 ,则点P的坐标是______。
,则点P的坐标是______。
答 案: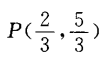
解 析: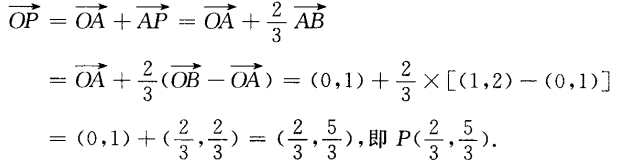
2、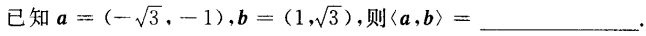
答 案:;150°
解 析: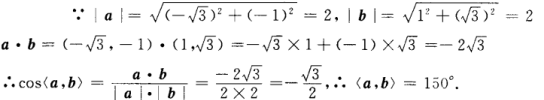
精彩评论