2025年成考高起点每日一练《数学(理)》5月13日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设函数f(x)=logax,且f(4)=2,则下列各式成立的是()。
- A:f(3)<O
- B:
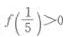
- C:f(5)<f(3)
- D:f(3)<f(5)
答 案:D
解 析:由f(4)-loga4=2,得a2=4,又a>0,故a=2,对于函数f(x)=logax,根据对数函数的性质有f(5)>f(3)成立.(答案为 D)
2、已知直线l:3x-2y-5=0,圆C: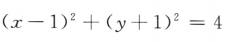 ,则C上到l的距离为1的点共有()
,则C上到l的距离为1的点共有()
- A:1个
- B:2个
- C:3个
- D:4个
答 案:D
解 析:由题可知圆的圆心为(1,-1),半径为2 ,圆心到直线的距离为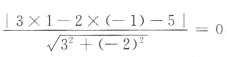 ,即直线过圆心,因此圆C上到直线的距离为1的点共有4个.
,即直线过圆心,因此圆C上到直线的距离为1的点共有4个.
3、设复数z1=1+2i,z2=2-i(其中i是虚数单位)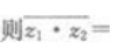 ()。
()。
- A:3-4i
- B:3+4i
- C:4-3i
- D:4+3i
答 案:C
解 析:z1•z2=(1+2i)(2-i)=4+3i,
4、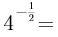 ( )
( )
- A:-2
- B:
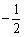
- C:
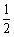
- D:2
答 案:C
主观题
1、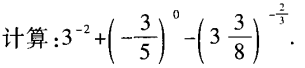
答 案: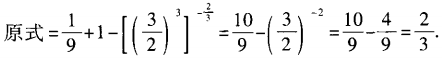
2、已知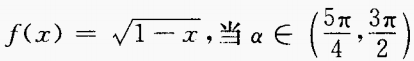 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 3、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。 答 案:由已知得 4、建筑一个容积为8000 答 案: 填空题 1、 答 案:1 解 析: 2、已知角α的终边过点P(-8m,-6cos60°)且cosα=- 答 案: 解 析:∵P(-8m,-3)且cosα=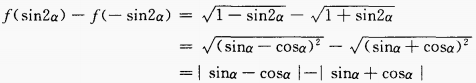
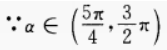 ∴sinα
∴sinα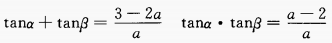

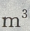 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每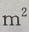 的造价为15元,池底每
的造价为15元,池底每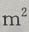 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
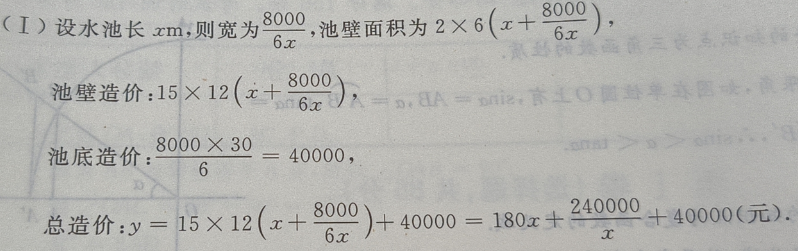

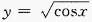 的定义域是______。
的定义域是______。
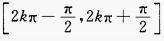
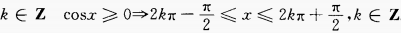
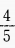 ,则m______。
,则m______。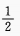
 ∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4
∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4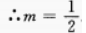
精彩评论