2025年成考高起点每日一练《数学(理)》5月20日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、下列各式中正确是()。
- A:
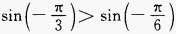
- B:
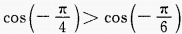
- C:
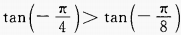
- D:
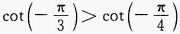
答 案:D
解 析: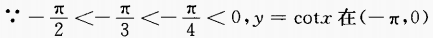 上为减函数,故
上为减函数,故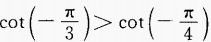
2、已知函数 则f(3)等于()。
则f(3)等于()。
- A:
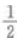
- B:1
- C:2
- D:
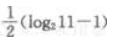
答 案:B
解 析: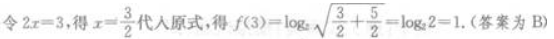
3、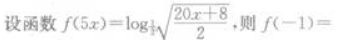 ()。
()。
- A:
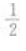
- B:
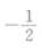
- C:2
- D:-2
答 案:B
解 析: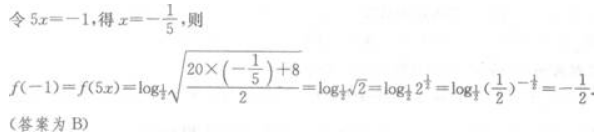
4、设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=()。
- A:-5
- B:5
- C:-10
- D:10
答 案:B
解 析:因为f(x)是偶函数,所以f(2)=f(-2)=5,又因为f(x)是以7为周期的函数,则f(9)=f(7+2)=f(2)=5。答案为B。
主观题
1、已知函数f(x)=(x-4)(x2-a) (I)求f"(x); (Ⅱ)若f"(-1)=8,求f(x)在区间[0,4]的最大值与最小值
答 案: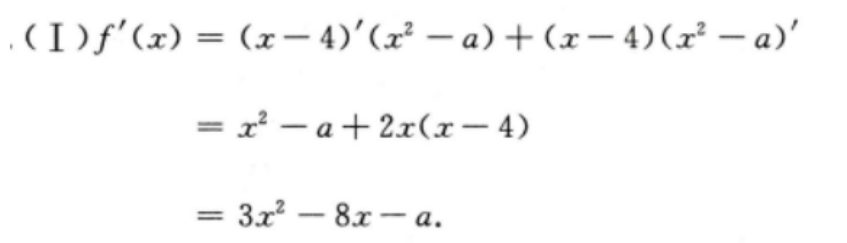

2、某气象预报站天气预报的准确率为80%,计算(1)5次预报中恰有4次准确的概率; (2)5次中至少有次准确的概率.(计算结果保留两个有效数字).
答 案: 把每次预报看做一次试验,“预报结果准确”看成事件P(A)=0.8,本题就相当于在5次独立重复试验中求A恰好发生4次(或至少4次)的概率,此题属于独立重复试验,由公式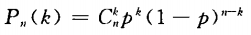 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4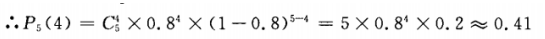 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即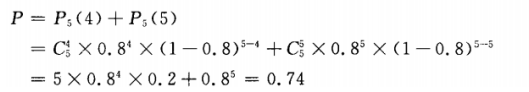 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
3、求下列函数的最大值、最小值和最小正周期: (1)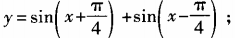 (2)y=6cosx+8sinx
(2)y=6cosx+8sinx
答 案:
4、已知数列{an}中,a1=2,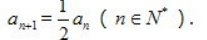 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
答 案:解:
填空题
1、已知sin2θ+1=cos2θ,则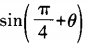 的值等于______。
的值等于______。
答 案:
解 析:由已知,cos2θ-sin2θ=1,即cos2θ-(1-cos2θ)=1,cos2θ=1,所以cosθ=±1。 而当cosθ=±1时,sinθ=0。 
2、函数y=2cosx-cos2x(x∈R)的最大值为______。
答 案: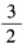
解 析: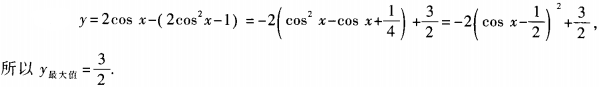
精彩评论