2025年成考高起点每日一练《数学(文史)》5月20日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设f(x)=1-f(x)log2x函数,则f(2)=()
- A:1
- B:-1
- C:2
- D:1/2
答 案:D
解 析:在f(x)=1-flog2x中令x=2得,f(2)=1-f(2)log22→f(2)=1-f(2)→1/2
2、已知|a|=4,|b|=5,向量a与b的夹角为π/3,则a·b的值为( )
- A:40
- B:20
- C:30
- D:10
答 案:D
解 析:根据两个向量的数量积公式a·b= 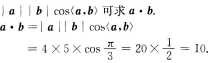 【考点指要】本题考查根据已知条件求两个向量的数量积,此类题是近几年成人高考的重点题.
【考点指要】本题考查根据已知条件求两个向量的数量积,此类题是近几年成人高考的重点题.
3、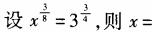 ()。
()。
- A:
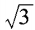
- B:9
- C:
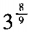
- D:
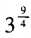
答 案:B
解 析:方法一:因为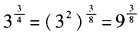 ,所以
,所以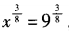 ,x=9,选B。 方法二:由题设,两边取以3为底的对数,得
,x=9,选B。 方法二:由题设,两边取以3为底的对数,得 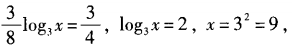
4、设甲:四边形ABCD是平行四边形,乙:四边形ABCD是正方形,则()。
- A:甲是乙的充分条件,但不是乙的必要条件
- B:甲是乙的必要条件,但不是乙的充分条件
- C:甲是乙的充分必要条件
- D:甲不是乙的充分条件,也不是乙的必要条件
答 案:B
主观题
1、设函数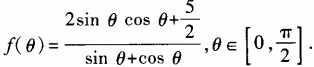 (1)求
(1)求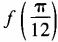 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
2、已知函数f(x)=2x3-3x2,求
(1)函数的单调区间;
(2)函数f(x)在区间[-3,2]的最大值与最小值。
答 案:
3、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。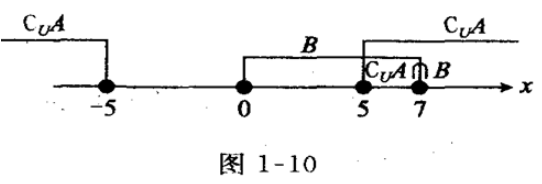
4、一艘渔船在航行中遇险,发出警报,在遇险地点西南10海里处有一艘货轮,接收到报时,发现遇险渔船正以9海里/小时的速度与沿南偏东75°方向向某小岛靠近,如果要在40分内将这艘渔船救出,求货轮航行的方向和速度。
答 案:货轮沿东偏北21.8°的方向,以21海里/小时的船速航行。
填空题
1、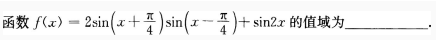
答 案: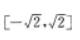
解 析: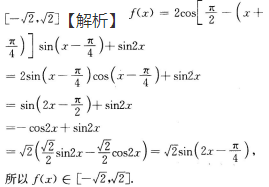 【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法,解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式,当函数可以化
【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法,解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式,当函数可以化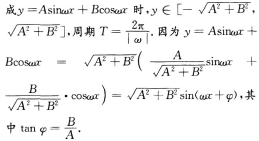
2、在△ABC中,AB=1, ______。
______。
答 案: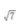
精彩评论