2025年成考高起点每日一练《数学(理)》5月26日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设F1,F2分别是椭圆的焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1,的面积等于()。
- A:
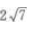
- B:
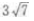
- C:
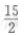
- D:2
答 案:B
解 析:
2、以椭圆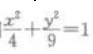 上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于()。
上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于()。
- A:
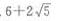
- B:
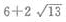
- C:
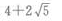
- D:
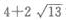
答 案:A
解 析:由椭圆方程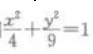 可知a2=9,b2=4,则
可知a2=9,b2=4,则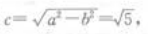 则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于
则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于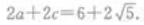
3、i为虚数单位,则复数 的虚部为()。
的虚部为()。
- A:
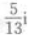
- B:
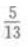
- C:

- D:
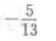
答 案:D
解 析:
4、已知正三棱柱的底面积等于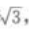 侧面积等于30,则此正三棱柱的体积为()。
侧面积等于30,则此正三棱柱的体积为()。
- A:
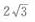
- B:
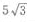
- C:
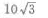
- D:
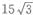
答 案:B
解 析:设正三梭柱的底面的边长为a,底面积为 设正三棱柱的高为h,侧面积为3×a×h=3×2×h=30,得h=5.则此正三棱柱的体积为底面积×高=
设正三棱柱的高为h,侧面积为3×a×h=3×2×h=30,得h=5.则此正三棱柱的体积为底面积×高=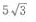
主观题
1、
答 案:
解 析:
2、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
3、试证明下列各题
(1)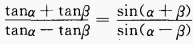
(2)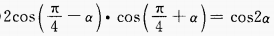
答 案:(1)化正切为正、余弦,通分即可得证。 (2)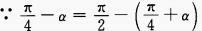

4、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
填空题
1、若tanα-cotα=1,则 =______。
=______。
答 案:4
解 析:由立方差公式得,tan3α-cot3α=(tana-cotα)(tan2α+tanαcota+cot2α)(tana-cotα)[(tanα-cotα)2+3tanαcotα]=4
2、长方体的长、宽、高分别为2,3,6,则该长方体的对角线长为()
答 案:7
解 析:由题可知长方体的底面的对角线长为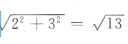 ,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为
,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为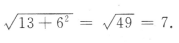
精彩评论